You are here
Aufgabe 100
Di, 2014-10-21 11:36 — richard
Aufgabe
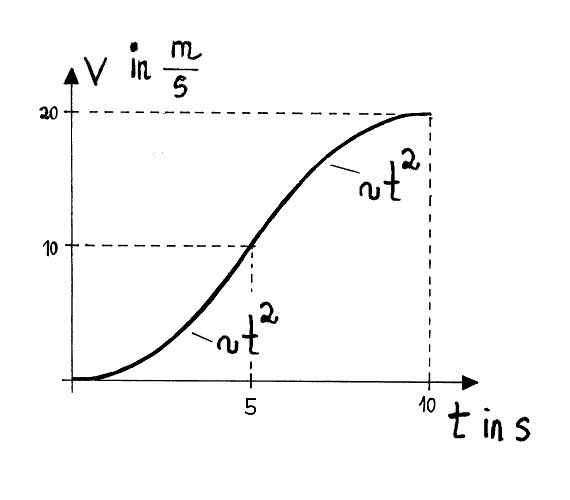
Ein Roller fährt vom Ort x=0m aus der Ruhe heraus $(v = 0 \frac m s)$ an. Nebenstehendes Bild zeigt seinen Geschwindigkeits-Verlauf.
Stellen Sie v(t) mathematisch dar. Berechnen und skizzieren Sie die Beschleunigung a(t).
Berechnen und skizzieren Sie die Wegbeschreibung x(t) zwischen 0s < t < 5s.
Bemerkungen
- Qualitative Interpretation: Der Roller beginnt mit $(v=0 \frac m s)$ und erreicht nach 10s die Geschwindigkeit $(v=20 \frac m s)$.
- Die Beschleunigung ist nicht gleichmäßig, sonst wäre diese Kurve eine Gerade und kein gebogenes "S"
Lösungsvorschlag:
>> Stellen Sie v(t) mathematisch dar.
Der hierzu entscheidende Hinweis dürfte das $\sim t^2$ in der Zeichnung sein. Also nehmen wir an, dass die Kurve im Schaubild jeweils von einem Teil einer Parabel $y=ax^2$ beschrieben werden soll.
Für t=0 bis t=5 setzen wir $y=ax^2$ an und setzen den Punkt (5|10) ein. Das ergibt $10 = a \cdot (5)^2$ oder nach "a" aufgelöst $a = 0.4$. Der untere Teil der Geschwindigkeits-Kurve kann also mit $v(t) = 0,4 \cdot t^2$ beschrieben werden.
Der obere Teil der Kurve von t=5 bis t=10 ist wieder eine Parabel. Diese hat die Öffnung nach unten (a<0), ist genausoweit aufgebogen und hat ihren Scheitel bei (10|20). Die allgemeine Scheitelform einer Parabel mit Scheitel im Punkt $(x_s|y_s)$ lautet $y=a(x-x_s)^2+y_s$. Demnach ist hier die Geschwindigkeits-Kurve durch $v(t) = -0,4 \cdot (x-10)^2+20$ beschrieben.
>> Berechnen und skizzieren Sie die Beschleunigung a(t).
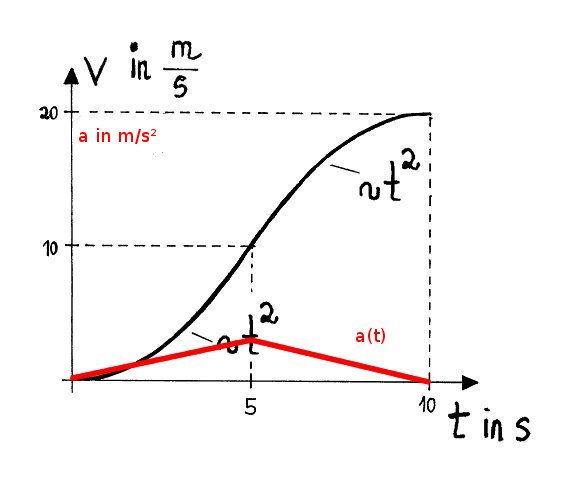 Die Beschleunigung ist die zeitliche Änderung der Geschwindigkeit, also ist die Beschleunigungsfunktion durch die Ableitung der Geschwindigkeitsfunktion beschreibbar.
Die Beschleunigung ist die zeitliche Änderung der Geschwindigkeit, also ist die Beschleunigungsfunktion durch die Ableitung der Geschwindigkeitsfunktion beschreibbar.
Für t=0 bis t=5 leiten wir $ v(t) = 0,4 \cdot t^2$ ab und erhalten $ \dot{v}(t) = \frac {dv(t)}{dt} = a(t) = 0,8 \cdot t$
Das ist (für t=0 bis t=5 )eine Gerade durch den Ursprung mit Steigung 0,8.
Für t=5 bis t=10 leiten wir $v(t) = -0,4 \cdot (x-10)^2+20 ~~=~~ -0,4 \cdot x^2 + 8 \cdot x - 20 $ ab und erhalten $ \dot{v}(t) = \frac {dv(t)}{dt} = a(t) = -0,8 \cdot t + 8$
Das ist (für t=5 bis t=10) eine Gerade mit Steigung -0,8 und dem v-Achsenabschnitt 8.
>> Berechnen und skizzieren Sie die Wegbeschreibung x(t) zwischen 0s < t < 5s.
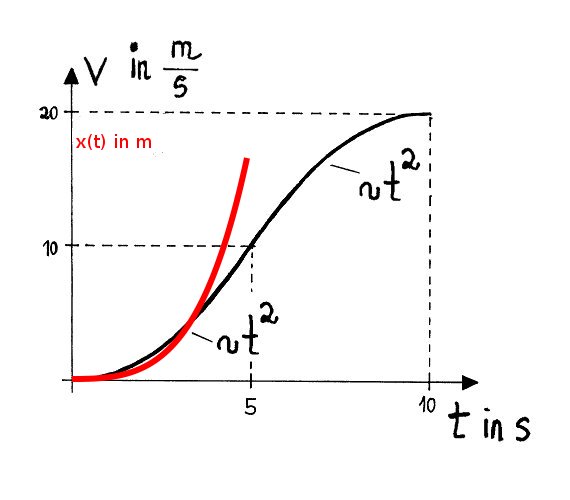 Die Geschwindigkeit ist die zeitliche Änderung der Strecke bzw. des Weges. Wenn ich also die Geschwindigkeitsfunktion habe und die Wegfunktion suche, dann muss ich eine Stammfunktion zur Geschwindigkeitsfunktion suchen.
Die Geschwindigkeit ist die zeitliche Änderung der Strecke bzw. des Weges. Wenn ich also die Geschwindigkeitsfunktion habe und die Wegfunktion suche, dann muss ich eine Stammfunktion zur Geschwindigkeitsfunktion suchen.
Eine Stammfunktion von $v(t) = 0,4 \cdot t^2$ wäre $\int v(t) dt = x(t) = \frac {0,4} {3} \cdot t^3$
- Log in to post comments
