Aufgabe 102

Aufgabe

Bei einem mathematischen Pendel hängt an einem Faden ein kleiner, aber schwerer Körper mit vernachlässigbarer Größe. Die
Geschwindigkeit dieses Massenpunktes wird durch die Beziehung

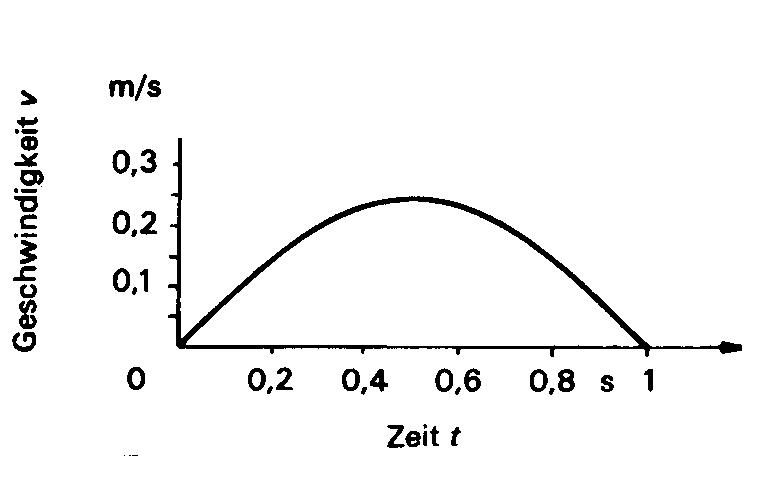
$v(t) = 0,25\frac{m}{s} sin(3.14\frac{1}{s} t)$

beschrieben und ist in nebenstehendem Bild dargestellt in der Zeit 0 ≤ t ≤ 1s.
Wie lautet der Ausdruck für die Beschleunigung a(t)? Wie groß sind die Extremwerte?

Lösungsvorschlag

>> Wie lautet der Ausdruck für die Beschleunigung a(t)?

$a(t) = \dot{v}(t) = \frac{dv(t)}{dt}~~=~~0,785\frac{m}{s^2}cos(3.14\frac{1}{s} t)$

>> Wie groß sind die Extremwerte?

Für den größten und kleinsten Wert der Beschleunigung a(t) setzt man die Ableitung  $\frac{da(t)}{dt} = -2,4649sin(3.14\frac{1}{s} t)~=~ 0$ und berechnet die Lösung(en) im Intervall 0 ≤ t ≤ 1s. Diese Gleichung ist für t=0 und für t=1 erfüllt (weil sin(0)=0 und sin(pi)=0).  Die Werte der Beschleunigung sind dann: $a(0)=0,785\frac{m}{s^2}$  und $a(1)=-0,785\frac{m}{s^2}$.

Für den größten und kleinsten Wert der Geschwindigkeit v(t) setzt man die Ableitung  $\frac{dv(t)}{dt} = a(t) = 0,785\frac{m}{s^2}cos(3.14\frac{1}{s} t)~=~ 0$ und berechnet die Lösung(en) im Intervall 0 ≤ t ≤ 1s. Diese Gleichung ist für t=0.5 erfüllt (weil cos(pi/2)=0).  Der Wert der Geschwindigkeit ist dann: $v(0,5)=0,25\frac{m}{s}$.